Представление вещественных чисел – одно из наиболее «темных» мест в современных учебниках информатики. Причин тут, видимо, много, в том числе не обходится без традиционного мотива «сложно это все, давайте объявим техническими деталями».

Считаю, что полноценный курс информатики невозможен без объяснения наиболее общих закономерностей представления вещественных чисел. Одного только знания принципов целочисленной арифметики недостаточно хотя бы потому, что целые числа дискретны, а вещественные непрерывны, так что вещественная арифметика будет обладать массой особенностей по сравнению с целочисленной!

Предлагаю читателям все-таки попробовать разобраться в основах представления вещественных чисел. Постараюсь со своей стороны сделать все, чтобы картина была максимально понятной, охватывала все наиболее важные идеи и, в то же время, не тонула в мелочах.

С точки зрения основной темы данной статьи, рассматриваемая проблема есть отличная иллюстрация того, что можно использовать Delphi для изучения вопросов, не входящих непосредственно в область языка Паскаль.

3.1. Основные принципы представления вещественных чисел

Начнем с того, что форма представления вещественных чисел придумана не «компьютерщиками», а математиками. В науке для записи очень больших и очень маленьких чисел уже давно используется способ, основанный на том, что любое число A в системе счисления с основанием B можно записать в виде

A = (±M) * B ^±P, где M называют мантиссой, а показатель степени P – порядком числа. Для десятичной системы это выглядит очень привычно, например: заряд электрона равен -1,6*10^-19 к, а скорость света в вакууме составляет 3*10⁸ м/сек. Обратите внимание, что мантисса – это по сути своей цифры числа, а порядок – величина, показывающая, в каком месте мантиссы надо поставить запятую.

Описанная выше система записи чисел называется представлением с плавающей запятой¹¹ (видимо, по той причине, что запятая «плавает» по мантиссе за счет порядка).

Некоторое неудобство вносит тот факт, что представление числа с плавающей запятой не является единственным:

3*10⁸ = 30*10⁷ = 0,3*10⁹ = 0,03*10¹⁰ = ...

Поэтому договорились для выделения однозначного варианта записи считать, что

• мантисса всегда меньше единицы (иначе говоря, целая часть равна нулю);
• старший разряд мантиссы содержит отличную от нуля цифру.

Такое представление чисел называется нормализованным и является единственным – в нашем примере обоим требованиям одновременно удовлетворит только 0,3*10⁹. Любое число может быть легко нормализовано. Единственное, но важное исключение из правила составляет нуль: в его мантиссе нет ни одной ненулевой цифры. Ради такого важного случая было введено дополнительное соглашение: число с нулевыми мантиссой и порядком (все биты – нули) в качестве исключения считать нормализованным.

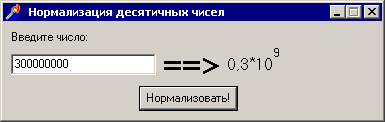
Рис. 7. Демо-приложение «Нормализация чисел»
(см. на диске)

Особо подчеркнем, что требования нормализации обеспечивают максимальную точность представления чисел. В частности, эта процедура эффективно убирает незначащие нули как из целой (1000000 = 0,1*10⁷), так и из дробной (0,0000001 = 0,1*10^-6) частей.

Все эти хорошо известные из математики(!) рассуждения могут быть применены и к двоичной системе счисления, лежащей в основе компьютерного представления чисел:

A = (±M) * 2 ^±P, Например: -3₁₀ = -11*2⁰ = -0,11*2¹⁰; отсюда M=0,11 и P=10.

В двоичной системе сформулированные выше требования нормализации приобретают новое, отсутствующее в десятичной системе, свойство. Согласно этим требованиям первый разряд мантиссы не должен быть равен нулю, что приводит к выводу, что он всегда равен единице (других-то цифр в двоичной системе нет!) Это позволяет при сохранении вещественных чисел в память не записывать заведомо известный старший разряд, а за счет освободившегося бита сохранить еще один дополнительный разряд мантиссы (разумеется, перед вычислениями в процессоре «отброшенная» «обязательная» единица восстанавливается). Такой метод хранения носит название «скрытая единица».

В отличие от математики, количество разрядов в изображении числа во всех вычислительных устройствах ограничено аппаратными возможностями (иначе говоря, разрядность хранения и обработки чисел конечна). При этом количество разрядов мантиссы (по сути, число знаков после запятой) влияет на точность вычислений, а разрядность порядка – на диапазон допустимых чисел. Мы подробнее изучим ограничения, которые возникают из-за конечной разрядности порядка и мантиссы вещественных чисел в экспериментах 6 и 7 соответственно.

И в заключение укажем на еще одну небольшую, но очень важную с практической точки зрения особенность устройства математического сопроцессора (без нее порядок всех переведенных «по большой науке» чисел всегда окажется на единицу больше). Дело в том, что при разработке сопроцессора было принято, что нормализованное число имеет одну единицу в целой части мантиссы¹² [9, 7], тогда как в «классическом» определении нормализации целая часть нулевая. Чтобы представить себе разницу, сравните две записи одного и того же числа; 0,1101*2¹⁰¹ и 1,101*2¹⁰⁰. Сопроцессор использует второй вариант.

Таким образом, в основе машинного представления вещественных чисел лежат следующие важные теоретические положения.

• Вещественное число хранится в виде двух компонентов – мантиссы и порядка. В мантиссе хранятся цифры числа, а порядок указывает на положение запятой.
• Для выделения некоторого единственного представления числа используются требования нормализации.
• Поскольку в двоичной системе старшая цифра нормализованной мантиссы всегда равна единице, при хранении чисел в технических устройствах ее можно отбрасывать (метод «скрытой единицы»).

3.2. Стандарт ANSI/IEEE 754-1985

Посмотрим теперь, как сформулированные теоретические принципы воплощаются в жизнь. Стандартом де-факто в этой области является Стандарт ANSI/IEEE 754-1985 [9], на базе которого, в частности, построен математический сопроцессор фирмы Intel. Как известно, сопроцессор этот является составной частью любого процессора, работающего внутри IBM-совместимого компьютера. (Попутный вывод: имеется «господствующая» система представления вещественных чисел, что повышает полезность ее изучения.)

Заметим, что в 2008 года ассоциация IEEE выпустила расширенный стандарт IEEE 754-2008 [10], который без изменений включил в себя стандарт IEEE 754-1985.

Согласно IEEE 754-1985, существует несколько форматов представления чисел. Все они показаны на рис. 8.

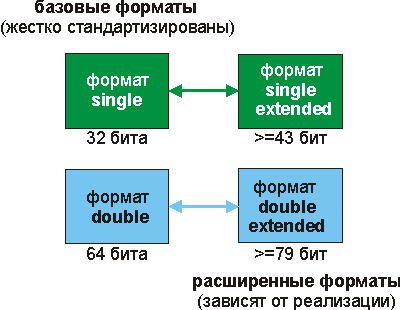
Рис. 8. Форматы вещественных чисел согласно Стандарту IEEE 754-1985

Базовые форматы служат для сохранения (и передачи) чисел. Для обеспечения максимальной совместимости данных, базовые форматы стандартизированы очень жестко (вплоть до бита). Что качается расширенных форматов, то они служат в основном для временного представления при обработке чисел¹³, поэтому они объявлены зависящими от конкретной реализации устройств (implementation-dependent) и для них в Стандарте описаны лишь самые общие требования.

Опираясь на полный перечень типов Стандарта IEEE 754, инженеры фирмы Intel при разработке своего математического сопроцессора упростили схему рис. 8 (не нарушая, разумеется, при этом Стандарта!) В итоге получилась схема взаимодействия типов, представленная на рис. 9.

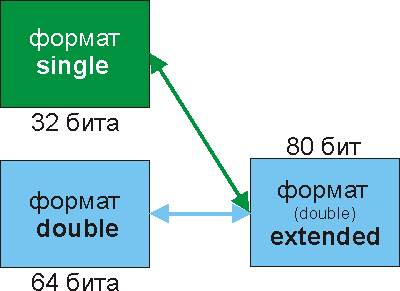
Рис. 9. Форматы вещественных чисел в математическом сопроцессоре фирмы Intel

Поскольку «младший» из расширенных форматов теперь упразднен, слово «double» в названии double extended становится излишним и постепенно отмирает.

Рассмотренная схема интересна для нашего обсуждения вот почему. Во-первых, она показывает, что существует два типа форматов: для хранения чисел (SINGLE и DOUBLE) и для их обработки (EXTENDED). Т.е. эти две группы форматов «не совсем родные» и могут иметь отличия. В сопроцессоре Intel, как оказалось, они действительно есть. Это должно повысить нашу подозрительность при чтении фраз типа «мы рассмотрели формат SINGLE, остальные форматы устроены совершенно аналогично» – совсем не обязательно, что совершенно аналогично. Во-вторых, тип EXTENDED в Стандарте описан очень поверхностно и для его подробного изучения надо обратиться к документации фирмы Intel (например, [11]). По моему мнению, перед нами возможные причины (хотя, может быть, и не все), по которым трудно найти хорошее и полное описание проблемы.

3.3. Вопросы разрядности

Согласно IEEE 754, любое вещественное число в форме с плавающей запятой состоит из трех компонентов: знака числа, порядка и мантиссы (рис. 10). Посмотрим, как распределяются биты между компонентами числа.

Рис. 10. Структура числа с плавающей запятой

Пусть общее количество битов B, причем нумеруются они по традиции с нуля. Если обозначить номер самого старшего бита мантиссы N, то количество битов мантиссы M = N+1. Количество битов порядка P при этом уже не может быть произвольным: оно вычисляется по формуле (B-1) – M. Распределение битов для всех типов рассматриваемых чисел представлено в следующей таблице (на последний столбец пока не обращайте внимание). Напомним, что значений последней строки таблицы в IEEE 754 нет.

тип числа	всего битов (B)	знаковый бит	битов в порядке (P)	битов в мантиссе (M)	применение "скрытой единицы"
SINGLE	32	1	8	23	да
DOUBLE	64	1	11	52	да
EXTENDED	80	1	15	64	нет

Знак всегда хранится в самом старшем бите и задается по правилу: 0 для положительных и 1 для отрицательных значений. При этом мантисса для положительных и для отрицательных значений кодируется одинаково (вспомним, что для отрицательных целых значений применялся специальный дополнительный код!)

Порядок также не лишен особенностей. Для того, чтобы избавиться от знака, его «сдвигают», прибавляя достаточно большое положительное число. В результате все отрицательные значения порядка исчезают, и он меняется от 0 до максимального значения¹⁴. Для чисел типа DOUBLE, например, величина сдвига выбирается равной 1023₁₀ = 3FF₁₆ (10 единичек из 11 разрядов порядка). Примеры расчета порядка с учетом сдвига мы рассмотрим позднее в 3.4 и 3.6.

А теперь поговорим о последнем столбике таблицы, ибо он того заслуживает. В очередной раз вернемся к мысли о том, что IEEE 754 строго регламентирует только базовые стандарты SINGLE и DOUBLE. В них метод «скрытой единицы» обязан применяться. Что же касается EXTENDED, то его детали оставлены на усмотрение разработчиков. Ну и как вы считаете, используется в формате EXTENDED «скрытая единица» или нет? Вот и я, честно говоря, до подготовки материалов статьи считал что используется¹⁵. А оказывается – нет! И вывод этот у меня возник в ходе одного из экспериментов.

Сейчас, «задним числом», я могу даже сказать, что сохранение всех разрядов мантиссы в рабочем формате EXTENDED даже объяснимо, поскольку это ускоряет вычисления... Зато неделю назад я верил тем, кто говорил, что «остальные форматы устроены совершенно аналогично»!

Эксперимент 5. Определение разрядности мантиссы

Проверим данные по распределению битов в вещественных числах, приведенные ранее в таблице. Особый интерес вызывает проверка разрядности мантиссы, поскольку размер порядка после этого однозначно определяется. Данный эксперимент кажется мне одним из наиболее изящных среди описанных в статье.

Постановка задачи. Экспериментально определить двоичную разрядность мантиссы для всех трех рассматриваемых типов вещественных чисел. Удобнее переформулировать задачу так: найти номер старшего бита мантиссы N. Если следовать общепринятой традиции нумерации битов с нуля, тогда разрядность мантиссы M = N+1 (см. рис. 10).

Реализация эксперимента. Программа, решающая поставленную задачу с некоторыми сокращениями приведена в листинге 5 (полный текст можно найти на диске). Исключена та часть, которая соответствует типу DOUBLE, поскольку она абсолютно аналогична разобранной части для SINGLE.

Листинг 5

var s: single; sb: integer absolute s; smask,n: integer; {здесь стояло несколько описаний для типа DOUBLE} dmask: int64; {для double и extended} ex: extended; exb: int64 absolute ex;

{мантисса у single} s:=0.75; {старший сохраненный бит мантиссы - 1, остальные - 0} smask:=1; n:=0; while (sb and smask)=0 do begin smask:=smask shl 1; n:=n+1; end; writeln('single: bit N ',n); {здесь стояла аналогичная программа для типа DOUBLE; ее можно посмотреть на диске!} {мантисса у extended} ex:=0.5; {старший бит мантиссы - 1, остальные - 0} dmask:=1; n:=0; while (exb and dmask)=0 do begin dmask:=dmask shl 1; n:=n+1; end; writeln('extended: bit N ',n); readln;

Разбор начнем с описательной части. Она отличается от всех предыдущих экспериментов тем, что на вещественные числа накладывается не массив из байтов, а подобранные по длине целые числа. Так, переменная s типа SINGLE совмещены с переменной sb типа INTEGER, т.к. оба типа 32-разрядные. Аналогичным образом DOUBLE хорошо совмещается с INT64. Труднее с типом EXTENDED: он 10-байтовый, а целого с такой разрядностью в Delphi нет¹⁶. Воспользуемся за неимением лучшего INT64. Подумаем, какую часть переменной ex он «накроет»? Младшие 8 байт, т.е. как раз всю ожидаемую мантиссу! (Надеюсь, вы не забыли об эффекте little-endian, благодаря которому байты в ОЗУ лежат «задом наперед», так что мантисса оказывается раньше порядка?) Итак, если мантисса не превысит 64 бит (а она теоретически не должна), наше решение сработает.

При объяснении программы оказывается гораздо проще начать обсуждение с последнего типа – EXTENDED, причем именно благодаря тому, что там «никто никуда не прячет» старший бит мантиссы. Напомню, мы хотим определить его номер.

План действий таков. Присвоим вещественной переменной значение 0,5₁₀ = 0,100..00₂. Очевидно, что его двоичная мантисса содержит все нули и единицу в старшем бите. Остается только найти номер этого бита.

Нам удалось свести задачу к хорошо известной. Она легко решается с помощью константы-маски с единственным ненулевым битом dmask и логической операции И. Из алгебры логики известно, что если в маске бит единичный, то результат равен значению бита числа, на которое эту маску накладывают. Для нулевого бита маски результат всегда нулевой и никак не зависит от исходного числа. Короче говоря описанная операция выделит из всего кода именно тот бит, для которого в маске установлена единица.

Первоначально маске dmask присваивается значение 1, что настраивает ее на самый младший (самый правый, с n=0) бит. Далее маска циклически накладывается на число exb и каждый раз проверяется равенство результата нулю (т.е. найдена единица или нет). Если бит оказался нулевым, то маска сдвигается на один разряд влево, номер бита n увеличивается на единицу и процесс повторяется еще раз. Так продолжается до тех пор, пока не будет обнаружена единица.

Подчеркнем, что операция И не может применяться к вещественным числам, так что если бы не наш трюк с absolute, ничего бы вообще не вышло!

Вернемся теперь к началу программы и поговорим о типе SINGLE. Здесь описанный выше алгоритм для числа 0,5 применить не удастся, поскольку старший бит мантиссы скрыт – просто нечего искать! Тем не менее, достаточно взять другое число – 0,75₁₀ = 0,110..00₂ и все сразу встанет на свои места: в мантиссе у 0,75 после того, как старший бит будет скрыт, останется единственная единица, причем она опять окажется в старшем бите.

Программа для DOUBLE устроена совершенно аналогично, изменятся только типы переменных. Особо подчеркнем, что алгоритм для SINGLE и DOUBLE ищет размер «сохраняемой» мантиссы, т.е. той, которая хранится в ОЗУ. Реальная мантисса числа на единицу («скрытую») больше.

Запустив программу, получаем следующие результаты:

single: bit N 22 double: bit N 51 extended: bit N 63

Все значения полностью согласуются с приведенными ранее в таблице, если учесть, что M = N+1.

Вывод. Полученные экспериментальным путем величины двоичной разрядности мантисс совпадают с приведенными в документации значениями.

3.4. Границы диапазона вещественных чисел

А помните, во введении речь шла о проблеме «самого маленького вещественного числа», которое можно сохранить в сопроцессоре и которое по разным данным имело самые разные значения? Давайте попробуем разобраться с этим. Как оказывается, тут есть о чем поговорить!

Мы уже знаем, что диапазон представления чисел зависит от разрядности порядка. Кроме того, нам известно, что порядок хранится со сдвигом, так что сохраняемое в ОЗУ значение порядка E_s = E + S, где E – значение порядка числа, а S – величина смещения, определяемая по формуле S = 2^Р–1 – 1. Если внимательно проанализировать последнюю формулу, то станет понятным, что смещение S равно примерно половине максимального значения порядка, так что в результате порядок меняется не от –Max до +Max, а от 0 до 2*Max (точнее будет сказать до 2*Max + 1).

Характеристики порядка для разных вещественных типов приведены в следующей таблице.

	SINGLE	DOUBLE	EXTENDED
разрядность порядка P, бит	8	11	15
диапазон порядка (IEEE 754)	-126..127	-1022..1023	-16382..16383
смещение S10	127	1023	(16383)17
смещение S2	111 1111	11 1111 1111	11 1111 1111 1111
смещение S16	7F	3FF	3FFF
количество бит смещения	7	10	14

Будем далее для примера рассматривать тип SINGLE; порядок для остальных типов устроен совершенно аналогично. Согласно IEEE 754, порядок для типа SINGLE может принимать значения от -126 до +127, так что смешенный порядок будет меняться от 1 до 254. Пусть, скажем, порядок некоторого числа равен 9. Тогда при сохранении в память его значение будет смещено и равно 9+127=136.

Из изучения двоичной системы мы четко помним, что беззнаковое положительное 8-битное число может принимать значения от 0 до 255. Между тем, смещенный порядок, как мы видели, охватывает диапазон от 1 до 254. Оставшиеся два значения (0 и 255) являются служебными и обрабатываются особо. Они имеют самое непосредственное отношение к нашему разговору о диапазоне представления чисел.

Рассмотрим, что происходит с числами, когда они становятся очень большими. Очевидно, что порядок этих чисел растет и в конце концов достигает 127 (смещенный порядок при этом стремится к значению 254). Когда мантисса достигнет своего максимального значения (все единицы), то число уже нельзя увеличить даже на единицу, не попадая в «запрещенное» значение смещенного порядка 255. Ситуация, когда число настолько велико, что не может поместиться в рамках существующей разрядной сетки, называется переполнением. Таким образом, появление в порядке значения 255 является для сопроцессора признаком переполнения. При этом значение, у которого порядок равен 255, а мантисса нулевая в IEEE 754 условно считается бесконечностью. Все же остальные числа с таким порядком обозначаются NaN (not a number – не число). Для работы с этими значениями в сопроцессоре приняты отдельные правила; мы не будем в них углубляться, а лучше поговорим об очень маленьких числах.

Итак, пусть теперь положительные числа уменьшаются. При этом их порядок становится все меньше и приближается к -126 (т.е. со смещением – к 1). В какой-то момент смещенный порядок равен 1, а мантисса содержит единственную единицу (по условиям нормализации – это старшая, она же – «скрытая» единица). Любая попытка еще уменьшить число (хотя бы на 1) приведет к появлению «запрещенного» нулевого значения в разрядах порядка. Казалось бы, результат придется обнулить, но тут инженеры Intel приготовили нам еще один сюрприз: числа с нулевым смещенным порядком продолжают обрабатываться, но по-другому! Поскольку порядок больше «не работает», то нормализацию приходится блокировать, а мантиссу обрабатывать «как есть». Фактически для очень маленьких чисел (по понятным причинам их называют денормализованными – нормализация не может использоваться!) сопроцессор переходит на другую модель вычислений: от плавающей запятой переходит к фиксированной. Это позволяет ему еще какое-то время «продержаться» и продолжать фиксировать ненулевые значению, но, в конце концов, мантисса обнулится, а число с нулевым порядком и мантиссой есть по определению машинный ноль.

Таким образом, мы получаем следующую последовательность чисел в сопроцессоре (от больших значений к меньшим):

NaN ––> бесконечность ––> нормализованные числа ––> денормализованные числа ––> ноль

Наличие отрицательных значений позволяет симметричным образом продлить эту последовательность:

-0 (минус ноль) ––> денормализованные и нормализованные числа ––> -бесконечность ––> -NaN

Минус ноль – это забавный казус: сопроцессор гарантирует, что -0 = +0. Прекрасная схема перечисленных типов с указанием их границ для типа SINGLE приведена в статье [7]:

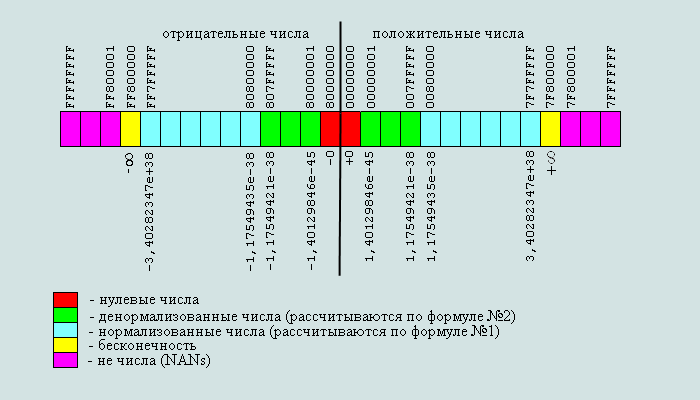
Рис. 11. Числа типа SINGLE в сопроцессоре [7]

Остается только научиться вычислять границы между типами, причем не только для типа SINGLE, но и для остальных.

Эксперимент 6. Границы диапазонов для вещественных чисел

Постановка задачи. Научиться вычислять изображенные на рис. 11 границы чисел для всех трех рассматриваемых вещественных типов.

Реализация эксперимента. Любая задача почти всегда может быть решена несколькими способами. В частности в статье [7] использован метод десятичных вычислений через степени двойки. Мне хочется предложить более простой метод, базирующийся на активно эксплуатируемой конструкции absolute.

Идея решения состоит в следующем. Все вычисляемые границы изначально пишутся в шестнадцатеричном виде, а нам надо перевести их в десятичный. Для этого совместим, как мы это уже неоднократно делали, вещественное число с байтовым массивом. Заполним массив необходимыми шестнадцатеричными значениями байтов, и нам останется просто напечатать вещественную переменную. Никаких формул и вычислений – сразу выводим ответ!

Решение для типов SINGLE и DOUBLE одинаковы с точностью до числовых значений, так что в листинге 6 оставлено только та часть, которая относится к SINGLE.

Листинг 6

var s: single; sb: array [1..4] of byte absolute s; {здесь стояли аналогичные описания для double} i:integer;

writeln('SINGLE:'); {минимальное денормализованное значение} {00 00 00 01} for i:=4 downto 2 do sb[i]:=0; sb[1]:=1; writeln('min denormalized: ',s); {максимальное денормализованное значение} {00 7F FF FF} sb[3]:=$7F; for i:=2 downto 1 do sb[i]:=$FF; writeln('max denormalized: ',s); {минимальное нормализованное значение} {00 80 00 00} sb[3]:=$80; for i:=2 downto 1 do sb[i]:=0; writeln('min normalized: ',s); {максимальное нормализованное значение} {7F 7F FF FF} sb[4]:=$7F; sb[3]:=$7F; for i:=2 downto 1 do sb[i]:=$FF; writeln('max normalized: ',s); {здесь стояла аналогичная программа для типа DOUBLE; ее можно посмотреть на диске!} readln;

Посмотрим, как устроен поиск границ. Самое маленькое денормализованное число, граничащее с нулем, есть единица в младшем разряде (00 00 00 01 для SINGLE). Самое большое денормализованное, напротив, содержит в мантиссе все единицы (но смещенный порядок остается нулевой: 00 7F FF FF). При переходе к нормализованным числам имеем порядок 1, а в мантиссе – единственную единицу, которую сопроцессор «скрывает»; проще говоря, сохраненная в память мантисса будет нулевой (00 80 00 00). Наконец, максимальное нормализованное число – это порядок 254₁₀ = FE₁₆ ¹⁸ и мантисса из единиц (7F 7F FF FF).

Для типа DOUBLE из-за различий в разрядности константы будут другие: 00 00 00 00 00 00 00 01, 00 0F FF FF FF FF FF FF, 00 01 00 00 00 00 00 00 и 7F EF FF FF FF FF FF FF соответственно. Сама программа устроена аналогично и поэтому в листинге не приведена.

После запуска программы на экране появятся следующие результаты.

SINGLE: min denormalized: 1.40129846432482E-0045 max denormalized: 1.17549421069244E-0038 min normalized: 1.17549435082229E-0038 max normalized: 3.40282346638529E+0038 DOUBLE: min denormalized: 4.94065645841247E-0324 max denormalized: 2.22507385850720E-0308 min normalized: 2.22507385850720E-0308 max normalized: 1.79769313486232E+0308

Сразу подчеркнем полное согласие полученных значений для SINGLE с приведенными на рис. 11 данными [7].

Отчетливо видно, что в качестве абсолютного минимума следует брать денормализованное значение. Денормализованный максимум и нормализованный минимум почти одинаковы, но последнее значение чуть-чуть больше. Между прочим, разница между ними не какая-нибудь, а равна именно абсолютному минимальному значению (см. на диске проект cmp_max_min). Таким образом, минимальное денормализованное значение оказывается важной характеристикой. С другой стороны, абсолютный максимум («значение перед самой сопроцессорной бесконечностью») есть максимальное нормализованное число.

Таким образом, границы типа SINGLE оказываются приблизительно равными 1,4*10^-45..3,4*10³⁸, а для DOUBLE – 4,9*10^-324.. 1,8*10³⁰⁸. Полученные степени полностью совпадают с приведенными в [8], хотя коэффициенты почему-то чуть-чуть отличаются. Еще раз подчеркнем, что наши коэффициенты очень хорошо совпадают с результатами [7].

Перейдем теперь к типу EXTENDED.

Главное отличие – это то, что старший бит мантиссы в граничных значениях требуется хранить. Поэтому программа для этого типа данных была написана отдельно (см. проект extended на диске), а значения шестнадцатеричных констант в ней были следующими: минимальное денормализованное значение 00 00 00 00 00 00 00 00 00 01, максимальное – 00 00 7F FF FF FF FF FF FF FF, минимальное нормализованное – 00 01 80 00 00 00 00 00 00 00 и, наконец, максимальное – 7F FF FE FF FF FF FF FF FF FF.

Ответы следующие:

EXTENDED: min denormalized: 3.64519953188247E-4951 max denormalized: 3.36210314311209E-4932 min normalized: 3.36210314311209E-4932 max normalized: 1.18973149535723E+4932

Полученный диапазон чисел: 3,6*10^-4951..1,2*10⁴⁹³². Сравнивая с таблицей [8], видим, что там в качестве нижней границы указано не минимальное ненормализованное, а минимальное нормализованное значение. Нет сомнения в том, что в Borland хорошо понимают, что такое денормализованные числа: просто Турбо Паскаль с ними не работает! (Подробнее об этом см. также в 3.7).

Кстати, значение степени, равное –4951, хорошо согласуется с оценкой в книге [1]. Чтобы быть еще больше уверенным в правильности вычислений, отдельные значения я пересчитал на встроенном в Windows калькуляторе. Оказалось, его точность выше(!), чем у Delphi и, соответственно, математического сопроцессора¹⁹. Вот, например, результат вычисления минимального нормализованного числа EXTENDED: 2^-16382 = 3,3621031431120935062626778173218e^-4932 (внушает?), т.е. 32 знака против 15 в Паскале. Зато все эти 15 совпадают в обоих ответах!

Выводы. В математическом сопроцессоре существуют две нижних границы для диапазона вещественных чисел – нормализованная и денормализованная (последняя ниже); денормализованные числа могут не поддерживаться программным обеспечением. Полученные результаты эксперимента тщательно проверены и имеют хорошую точность. Самое маленькое вещественное число приблизительно равно 3,6*10-4951.

3.5. Точность представления вещественных чисел

В предыдущем примере нам удалось экспериментально определить диапазон представления чисел, используя знание разрядности порядка. Аналогичным образом стоит изучить и разрядность мантиссы, что позволит оценить точность вычислений каждого из вещественных типов в десятичных знаках.

Прекрасная идея эксперимента была описана в недавней публикации [6]. Его суть состояла в следующем. Берем вещественное число, равное 1, и прибавляем к нему некоторую добавку, вычисляемую по формуле 2^-n: 1/2, 1/4, ... При этом бинарная мантисса числа ведет себя так: 1,1, 1,01, ..., 1,00..01. Очевидно, что в какой-то момент младшая единица «вылезет» за разрядную сетку и «потеряется». Сумма перестанет отличаться от единицы, что и зафиксирует программа.

В [6] было продемонстрировано, что погрешность вычислений не зависит от типа вещественных данных, поскольку все они ведутся в формате EXTENDED. Немного модифицировав предложенную авторами программу, все-таки можно измерить разницу в точности использования вещественных переменных разных типов: для этого надо обязательно сохранять результат суммирования в память. Думается, эксперимент 7 стоит сделать хотя бы для того, чтобы избежать неверного вывода о том, что для всех типов вещественных переменных погрешность одинакова (если бы это было так, то все бы пользовались самым коротким типом SINGLE!)

Эксперимент 7. Определение десятичной разрядности мантиссы

Постановка задачи. Определить, с какой погрешностью работают программы, построенные на каждом из рассматриваемых вещественных типов данных. Результат погрешности вычислить в десятичной системе.

Реализация эксперимента. Фрагмент модифицированной программы из [6], относящийся к типу SINGLE, воспроизведен в листинге 7. Программа была реализована в системах Free Pascal (файл epsilon2.pas на диске) и Delphi (проект также есть на диске).

Листинг 7

program for_Free_Pascal var s,es:single; d,ed:double; e,ee,n:extended; begin n:=1; {по n был цикл} writeln('n=',n:2:0); writeln('SINGLE'); s:=1; repeat s:=s/2; es:=n+s until es=n; writeln(s/n); {здесь стояли аналогичные программы для DOUBLE и EXTENDED; их можно посмотреть на диске!} readln; end.

При запуске программы на экране появились следующие результаты:

n= 1 SINGLE 5.9604644775390625E-0008 DOUBLE 1.1102230246251565E-0016 EXTENDED 5.4210108624275222E-0020

Видно, что точность вычислений с применением переменных, разумеется, зависит от разрядности вещественного типа (часть разрядов теряется при сохранении чисел в ОЗУ). Хочется отметить прекрасное согласие полученных результатов с уже упоминавшейся ранее таблицей из [8]. Там, в частности, сказано, что тип SINGLE гарантирует 7-8 значащих цифр, DOUBLE – 15-16, а EXTENDED – 19-20.

Отдельно надо сказать о роли переменной n. С ее помощью можно прекрасно продемонстрировать, что относительная погрешность вычислений с плавающей запятой постоянна [6]. Вычисления показывают, что при n=1, 2, 4, ... (степени двойки) отношения погрешности к величине числа n получаются абсолютно одинаковыми. Да и как может быть иначе, если фактически речь идет о числах с идентичной мантиссой, различающихся только порядком!

Возможно, некоторые читатели спросят: а почему бы и здесь не использовать нашу «абсолютную» технологию (в смысле, с оператором absolute)? Как сейчас принято говорить в молодежных кругах – легко!

Для этого достаточно составить шестнадцатеричное представление числа 1,0 и в самом последнем его бите дописать единицу. Разность между этим числом и единицей и есть искомый результат.

К сказанному остается только добавить, что в формате SINGLE вещественная единица имеет код 3F 80 00 00, DOUBLE – 7F F0 00 00 00 00 00 00, и, наконец, в EXTENDED – 3F FF 80 00 00 00 00 00 00 00.

Фрагмент программы, который относится к типу SINGLE (для остальных типов программа устроена аналогично) приведен на листинге 8. Как обычно, «желтую» описательную часть вставляем в текст проекта до begin, а операторную – после него.

Листинг 8

var s: single; sb: array [1..4] of byte absolute s; {здесь стояли аналогичные описания для double}

writeln('SINGLE:'); {3F 80 00 01 единица "с хвостиком"} sb[4]:=$3F; sb[3]:=$80; sb[2]:=0; sb[1]:=1; writeln(s-1); {здесь стояли аналогичные программы для DOUBLE и EXTENDED; их можно посмотреть на диске!}

Запускаем, и получаем те же самые… А вот и нет! Результаты оказываются ровно вдвое больше:

SINGLE: 1.19209289550781E-0007 DOUBLE: 2.22044604925031E-0016 EXTENDED: 1.08420217248550E-0019

Впрочем, неожиданно это только на первый взгляд. На самом деле, это понятный эффект, связанный с устройством алгоритмов листингов 7 и 8. В первом из них печатается первое число, для которого не была зафиксирована разница с единицей ²⁰, а во втором – последнее, которое еще отличается от единицы.

Полученные степени сравним по порядку величины со степенями «исчезновения порядка» в предыдущем эксперименте: последние значительно выше! Это означает, что ограничения точности, связанное с мантиссой, проявляется существенно раньше, чем для порядка. Страшно ли это для вычислений? Вспомните, для примера, типовые задачи, которые вы решали на уроках физики. Как правило, вычисления там ведутся по формулам, которые представляют собой дробь с произведениями величин в числителе и знаменателе. Из математической теории известно (см., например, [3]), что погрешность в такой ситуации определяется исключительно числом с минимальным количеством знаков после запятой! Проще говоря, если в одном из чисел достоверно известны только 2 знака, а у всех остальных – 8, в ответе все равно будут верными только 2 цифры после запятой. А теперь вспомните – сколько знаков вы используете в вычислениях на физике? Едва ли больше 3-4, а то и вовсе 1-2! Так что погрешность мантиссы в самом плохом случае в восьмом десятичном знаке едва ли вас должна настораживать. Зато диапазон значений вам требуется немалый: двузначный десятичный порядок – это не исключение, а, скорее, правило в микромире (отрицательные порядки) и в астрономических масштабах (положительные). Таким образом, оказывается, что принятое в компьютере распределение разрядов под мантиссу и порядок вполне разумно.

Выводы. Точность хранения в памяти переменных разных типов различна, хотя вычисления в сопроцессоре для всех ведутся с одинаковой точностью. Полученные в эксперименте 7 значения хорошо согласуются с известными из других источников данными.

3.6. Как перевести число?

В предыдущих разделах мы подробно изучили общие принципы представления вещественных чисел в компьютере. Видимо, настала пора применить эти принципы на практике. Сначала попробуем на листке бумаги, а потом перейдем к программному обеспечению.

Допустим, требуется представить в двоичном виде вещественное число -17,25. Выберем для простоты тип SINGLE как имеющий самый короткий по длине записи формат.

Прежде всего, переведем модуль числа, т.е. 17,25, в двоичную форму, как этому учит математическая теория: отдельно целую, и отдельно дробную части. В итоге получим:

10001,01

Нормализуем полученное число. Для этого согласно общепринятому определению потребовалось бы передвинуть запятую на 5₁₀ = 101₂ разрядов влево, но в сопроцессоре принято старшую единицу выносить в целую часть (см. 3.1), поэтому получим:

10001,01*2⁰ = 0,1000101*2¹⁰¹ = 1,000101*2¹⁰⁰

Остается сформировать мантиссу, «скрыв» старшую единицу:

M = 0,000101

Как мы помним, в отличие от целых чисел, где отрицательные числа представляются в дополнительном коде, мантисса вещественных чисел хранится в прямом коде. Следовательно, больше никаких преобразований мантиссы не требуется.

Знаковый разряд необходимо установить в 1, поскольку число отрицательное: Z = 1. Теперь остается закодировать двоичный порядок 100. Для хранения порядка в числах типа SINGLE смещение равно 7F (см. таблицу в 3.4), так что смещенный порядок будет равен

E_S = 100 + 111 1111 = 1000 0011

Собирая теперь Z, E_S и M в единое 32-разрядное число, окончательно получаем:

1 10000011 0001010 00000000 00000000 Или более компактно в шестнадцатеричной системе – C1 8A 00 00. Этот код и будет записан в ОЗУ, правда байты при этом, как мы знаем, будут переставлены.

Не думаю, что описанная процедура сложна по своей сути, но технической работы требуется много. А значит, велика вероятность ошибиться. Поэтому для проверки неплохо бы иметь специальное учебное программное обеспечение, способное для введенного десятичного числа выдать его внутренне представление и, наоборот, расшифровать прочитанные из ячеек ОЗУ значения. Этим мы сейчас и займемся.

3.7. Инструмент для изучения представления вещественных чисел

Я очень боюсь, что разочаровал читателей. В заголовке стоит Delphi и многие, вероятно, ожидали многочисленных окон, кнопок, флажков и прочих визуальных объектов. А вместо этого им предложили многочисленные консольные приложения в черном окне, которое многие сейчас воспринимают как призрак умирающей MS-DOS. Еще раз подчеркну, что все рассмотренные ранее примеры не требовали практически никакой интерактивности и просто выводили на экран некоторые числа. Кроме того, как случайно оказалось (и скоро мы это увидим), в графических приложениях менее точно, чем в консольных, реализована работа с числами типа EXTENDED. А это уже для нас принципиально.

Но, тем не менее, обманывать ожидания читателей нехорошо. К тому же мы подошли к достойной задаче, в которой возможностью удобно вводить данные пренебрегать нельзя. И сейчас мы, наконец(!), напишем настоящее графическое приложение.

Учебная программа «FPview»

Постановка задачи. Реализовать учебную программу, которая по введенному десятичному числу выдает его внутренне представление и, наоборот, расшифровывает введенный шестнадцатеричный код в виде вещественного числа.

Проект. Для простоты сначала реализуем простейшую версию программы. Назовем ее FPview_micro – просмотрщик вещественных (floating-point) чисел. Эту версию программы мы разберем, хотя и с некоторыми сокращениями. Зато более мощную (мини-версию) мы обсудим только с пользовательских позиций. Желающие смогут заглянуть в «исходники» этого проекта на диске и изучить его.

Итак, создадим настоящее Windows-приложение (application) и сконструируем для него простейшую заготовку окна (форму Form1), примерный вид которой приведен на рис. 12.

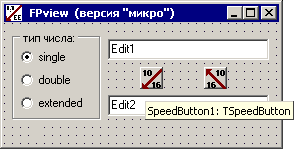
Рис. 12. Вид формы проекта

На форме созданы следующие компоненты. Во-первых, два поля редактирования – Edit1 и Edit2, в которые будем вводить десятичное число или шестнадцатеричный код соответственно. В этих же полях будут отображаться результаты перевода. Например, когда мы введем в Edit1 интересующее нас десятичное число, приложение в Edit2 выведет его машинное представление и наоборот.

Во-вторых, предусмотрим две кнопки типа TSpeedButton для перевода из одной формы в другую. Будем условно обозначать 10 ==> 16 перевод из вещественного числа в машинное представление, а 16 ==> 10 – обратный процесс.

Наконец, слева на форме находится переключатель типов чисел RadioGroup1, на котором перечислены все три изучаемых нами типа.

Учитывая простоту проекта, в нем будет всего два обработчика событий – на каждую из кнопок.

Перейдем к чтению и анализу текста программы. С некоторыми сокращениями он приведен на листинге 9. Сокращению подверглись в основном второстепенные с точки зрения основного алгоритма функции и процедуры. Я надеюсь, что функция, которая преобразует число типа byte в два шестнадцатеричных символа и обратная ей – это не то, что стоит сейчас подробно обсуждать. К тому же недавно появившееся в газете приложение в виде компакт-диска – это спасательный круг для меня как для автора: теперь, поместив полный текст программы на диске, я могу больше не беспокоиться о том, что без не попавших на страницы газеты кусков программа работать не будет!

Листинг 9

type float_type=(fs,fd,fe); {single, double, extended} {количество байт в представлении типов} const NB: array [float_type] of integer = (4, 8, 10); var s: single; sa: array [1..4] of byte absolute s; d: double; da: array [1..8] of byte absolute d; e: extended; ea: array [1..10] of byte absolute e; errFlag: boolean; {флаг ошибок при переводе 16 ==> 10} function MyByteToHex(n:byte):string; {выдает 16-код заданного байта} begin {текст функции см. на диске} end; procedure TForm1.SpeedButton1Click(Sender: TObject); {перевод 10 ==> 16} var w: array [1..10] of byte; {копия байтов числа} hex,sobr: string; i,n: integer; begin case radioGroup1.ItemIndex{single, double, extended} of 0: begin s:=StrToFloat(edit1.Text); {введенное число} n:=Nb[fs]; {количество байт} {копируем байты числа в рабочий массив} for i:=1 to n do w[i]:=sa[i]; end; {0} 1: begin d:=StrToFloat(edit1.Text); n:=Nb[fd]; for i:=1 to n do w[i]:=da[i]; end; {1} 2: begin e:=StrToFloat(edit1.Text); n:=Nb[fe]; for i:=1 to n do w[i]:=ea[i]; end; {2} end; {case} sobr:=''; for i:=1 to n do {побайтная обработка} begin {перевести в 16-код очередной байт} hex:=MyByteToHex(w[i]); {значения байтов в обратном порядке} sobr:=hex+' '+sobr; end; edit2.Text:=sobr; end; function MyHexToByte(s:string):byte; {выдает целое значение, соответствующее 16-коду байта} begin {текст функции см. на диске} end; function check_length(var w: string; b: integer):boolean; {проверяет длину текста, сравнивая с удвоенным числом байт; дополняет нули слева или обрезает строку, всегда спрашивает согласия пользователя} begin {текст функции см. на диске} end; procedure TForm1.SpeedButton2Click(Sender: TObject); {перевод 16 ==> 10} var w1,w2: string; i,n: integer; t: float_type; begin w1:=edit2.Text; {удалить пробелы} while pos(' ',w1)<>0 do delete(w1,pos(' ',w1),1); {перебираем типы, пока номер не совпадет с itemIndex} t:=fs; while ord(t)<>radioGroup1.ItemIndex do t:=succ(t); n:=Nb[t]; {количество байт для данного типа} {проверим длину} errFlag:=not check_length(w1,n); if errFlag then begin Edit1.Text:=('Terminated by user'); exit end; {пакуем байты из строки в память в обратном порядке} for i:=1 to n do {перебираем байты} begin {берем очередной и удаляем из исходной строки} w2:=copy(w1,1,2); delete(w1,1,2); case t of fs:begin {пакуем в память} sa[n+1-i]:=MyHexToByte(w2); {отображаем результат} edit1.Text:=FloatToStr(s); end; fd:begin da[n+1-i]:=MyHexToByte(w2); edit1.Text:=FloatToStr(d); end; fe:begin ea[n+1-i]:=MyHexToByte(w2); edit1.Text:=FloatToStr(e); end; end; end; if errFlag then edit1.Text:=('Error!') end; end.

Программа начинается с описаний исследуемых переменных SINGLE, DOUBLE и EXTENDED, на которые, как мы это уже неоднократно делали, наложены байтовые массивы соответствующей длины. В первый момент я хотел совместить их сразу все, но затем осторожность взяла верх, и я объединил их попарно.

Далее в тексте программы помещен обработчик первой кнопки, при нажатии которой происходит перевод 10 ==> 16.

В соответствии с состоянием RadioGroup1 (а точнее, со значением номера нажатой радиокнопки ItemIndex) из трех ветвей алгоритма выбирается та, которая соответствует выбранному вещественному типу. Пусть, например, выбран тип SINGLE, которому соответствует нулевое значение индекса. Тогда считанная с поля редактирования Edit1 строка преобразуется в значение числа стандартной функцией StrToFloat() и сохраняется в переменную s. Заметим, что в использованной функции уже заложен контроль возможных ошибок в записи числа, так что никаких дополнительных действий с нашей стороны не требуется. Как только переведенное значение попало в переменную, можно сразу же пользоваться содержимым байтового массива sa, с ней совпадающим. Для того, чтобы в дальнейшем работать с одним массивом, а не выбирать все время нужный из трех, скопируем все n байтов массива sa в рабочий массив w. После этого все три ветви алгоритма «сливаются» в одну общую.

Завершающая часть обработчика преобразует набор целых чисел из массива w в текстовую строку sobr, куда шестнадцатеричные эквиваленты байтов заносятся в обратном порядке («компенсация» эффекта little-endian). Окончательную строку заносят в свойство Text компонента Edit2, и пользователь видит результат перевода на экране.

Перейдем теперь ко второму (обратному) обработчику. Он начинается с того, что считывает исходную строку из свойства Text компонента Edit2 в переменную w1, с которой программа в дальнейшем и работает. Сначала производится целый ряд несложных, но полезных вспомогательных действий. В частности, из строки удаляются все пробелы, что уменьшает вероятность появления ошибок из-за невнимательности пользователя. Далее располагается немного «непрозрачный» цикл, суть которого крайне проста: перевести числовой номер RadioGroup1.ItemIndex в значение типа fs, fd или fe. Для этого с помощью функции succ(), т.е. следующий, они по очереди перебираются и номер текущего значения сравнивается с ItemIndex. В момент совпадения (а его не может не быть, поскольку и радиокнопок, как и типов ровно три!) цикл немедленно завершается и в переменной t сохраняется наименование выбранного пользователем типа. Зная это значение, можно считать из массива количество байт Nb, а также в дальнейшем обращаться к одной из трех переменных, s, d или e которая имеет необходимый тип.

После этого вызывается еще одна проверочная процедура, цель которой сравнить длину полученной строки и количество байт для выбранного типа данных. В идеале длина в точности равна удвоенному количеству байт, т.к. каждый из них записывается двумя шестнадцатеричными цифрами. Если оказывается, что реальная строка короче, компьютер предлагает пользователю автоматически дописать слева необходимое количество нулей. В противном случае, предлагается «укоротить» строку до необходимой длины. В обоих случаях с помощью очень удобной функции MessageDlg() у пользователя запрашивается подтверждение на изменение строки. Пользователь может отказаться от предложения «испортить» его строку; в этом случае функция check_length() возвращает значение false и выполнение обработчика прерывается.

Если же с длиной все прошло удачно, программа продолжает свою работу. Из строки w1 последовательно извлекается по две шестнадцатеричных цифры, которые преобразуются в целочисленное значение типа byte и пакуются в нужный массив (выбор массива соответствующего типа происходит по переменной t, о которой подробно рассказывалось выше). Главная «хитрость» данного цикла состоит в том, что заполнять массив приходится «с конца» с тем, чтобы изменить порядок байтов на противоположный.

В ходе перевода какой-то из обрабатываемых символов может оказаться некорректным. В этом случае в одной из внутренних процедур переменная errFlag получит значение false. Последний оператор обработчика обеспечит в этом случае индикацию ошибки.

Вот так вкратце и устроена программа.

Запустим ее и протестируем. В качестве тестов можно использовать результаты, полученные ранее в 3.4 и 3.6. Кроме того, полезно заранее «вручную» перевести 2-3 значения чисел и потом их проверить. Все должно прекрасно получаться, кроме одного: любое денормализованное число в режиме EXTENDED программа принципиально сбрасывает в ноль²¹! Очень любопытный результат! Как тут не вспомнить таблицу границ значений из [8], о которой мы уже столько говорили. В ней честно сказано, что нижняя граница EXTENDED совпадает с наименьшим нормализованным числом. Т.е. это не ошибка, а так задумано.

А как же все-таки в Delphi обстоит дело с ненормализованными значениями? С чувством глубокого удовлетворения сообщаю, что наша программа в состоянии помочь ответить на этот вопрос. Давайте дадим ей некоторое десятичное значение, скажем, 1e-4949, которое заведомо является денормализованным (проверьте по данным 3.4). Ответ, воспроизведенный на рис. 13, приятно радует: значение будет ненулевым! (Правда, при обратном переводе десятичное число немедленно обнуляется.) Таким образом, эксперимент убедительно показывает, что в памяти такие значения хранятся, но при выводе обнуляются. Тем более забавно, что в компилируемых в Delphi консольных приложениях оператор WRITE прекрасно справляется с выводом обсуждаемых значений на экран²²!

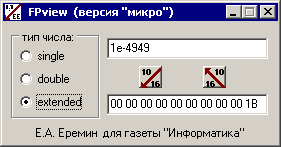
Рис. 13. А денормализованные значения все-таки есть!!!

Полученная в результате трансляции листинга 9 программа уже существенно помогает в изучении представления вещественных чисел. В частности, она позволяет проверить правильность «ручного» перевода при подготовке примеров, а также незаменима при составлении и проверке решения задач. Тем не менее, выводимый шестнадцатеричный код нужно еще расшифровывать. Неплохо было бы, если бы программа помогала и здесь. Нужна новая, более мощная версия, способная делать это. И она тоже предлагается вашему вниманию, правда, на уровне пользовательского описания. Полный текст проекта содержится на диске. Я бы посоветовал заглянуть в текст проекта: если вам нравится программирование, вы можете найти там для себя кое-что интересное (скажем, массив из визуальных компонентов или широкое применение логических операций при формировании чисел).

Новая версия, вид окна которой показан на рис. 14, выглядит существенно привлекательнее, чем аскетичная версия «микро».

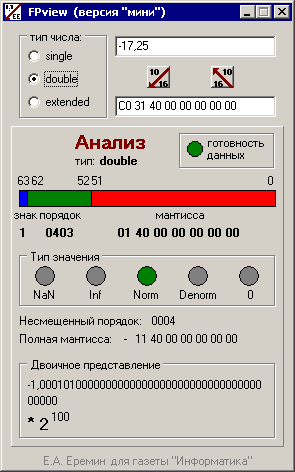
Рис. 14. Расширенная версия программы

Сразу бросается в глаза, что большую часть окна в новой версии занимает панель, на которой отображаются результаты анализа кода числа. На ней можно прочесть:

• тип вещественного числа;
• распределение битов кода для этого типа;
• значения знакового бита и битов порядка и мантиссы, выделенные из кода введенного числа;
• тип значения (NaN, бесконечность, нормализованное, денормализованное или машинный ноль);
• истинное значение порядка, полученное после вычитания смещения;
• полное значение мантиссы, включая восстановленную «скрытую единицу» (если она была скрыта);
• окончательно расшифрованное двоичное число.

На рис. 14 изображено окно с информацией о числе -17,25 формата DOUBLE (ранее в 3.6 оно переводилось в SINGLE). Легко убедиться, что отображаемое в нижней части окна расшифрованное двоичное число действительно соответствует результатам перевода указанного десятичного числа в двоичную систему счисления.

Пара слов по поводу «таинственного» индикатора готовности данных в правой верхней части панели. Все данные панели автоматически отображаются после нажатия любой из двух кнопок перевода. Представим теперь, что мы изменили состояние радиокнопок или начали изменять содержимое поля редактирования с десятичным числом. Данные на панели анализа пока сохраняются без изменения. В результате содержимое верхней и нижней частей окна перестают соответствовать друг другу, о чем будет напоминать пользователю красный цвет индикатора. После завершения ввода изменений и нажатия на любую из кнопок перевода индикатор снова «позеленеет», что будет свидетельствовать об обновлении данных на панели анализа²³.

Возможно, читателей заинтересовало, почему версия названа «мини» и чего же еще в ней не хватает. Как показало тестирование, Delphi не всегда корректно обрабатывает «неправильные» значения двоичных кодов, занесенные в качестве вещественных значений. Например, программа «ругается» на значение single-NaN, равное FF 90 00 00, или некорректное extended-значение 40 00 00 00 00 00 00 00 00 00 (в нем отсутствует «нескрываемая» единица в мантиссе, чего быть не должно). К тому же, как указывалось ранее, Delphi не поддерживает ненромализованные extended-значения, принудительно их обнуляя при выводе. И хотя все это весьма второстепенные ограничения, полноценная программа все это должна как-то делать. Еще возникало желание добавить возможность ввода двоичного числа в виде X * 2^Y в нижней части окна. В общем, нет в мире совершенства...

Возможно, вам покажется интересным сравнить возможности описанного в статье инструмента с уже имеющимися, например, с online-версией конвертера [12].

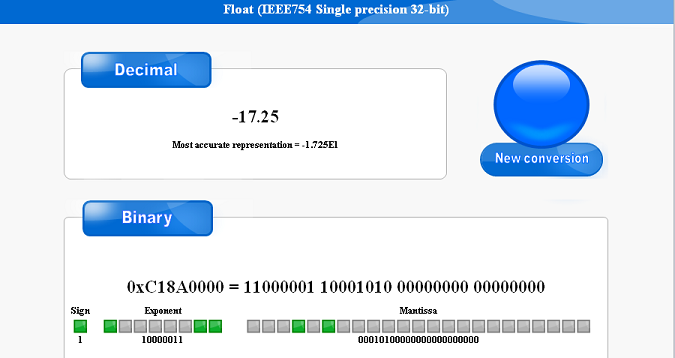
Рис. 15. Online конвертер для вещественных чисел [12]

3.8. «Бонусный» эксперимент

Часто в компьютерных играх после прохождения серии трудных уровней предлагается так называемый бонус (призовая стадия), которая позволяет расслабиться, прежде чем двигаться дальше. Мне хочется предложить тем, кто добросовестно разбирался во всех хитросплетениях вещественных чисел проделать следующее простое и забавное упражнение. Откройте стандартный калькулятор Windows (в инженерном режиме) и попробуйте получить вещественное число, которое изображено в копии экрана на рис. 16.

Рис. 16. Калькулятор Windows способен обрабатывать огромные вещественные числа

Трудность в том, что набор порядка ограничен четырьмя цифрами, после чего компьютер начинает «возмущенно пищать» и игнорирует дальнейший набор. Не сомневаюсь, что, используя свои математические знания, читатели легко справятся с предложенным «бонусным» упражнением. И тем, кто это сделает – «призовая картинка». Возведите число, изображенное на экране, в квадрат 5-6 раз. Забавное диалоговое окно, которое вы увидите, вполне способно вызвать положительные эмоции. Во всяком случае, я хорошо посмеялся.