Среди всех школьных учебных пособий, которые автор просмотрел, подбирая материал по данному вопросу, наиболее полной оказалась книга [1] (учитывая главу с дополнениями во второй части). Хорошим источником информации может служить книга [2], посвященная вопросам изучения машинной арифметики. Некоторые интересные ссылки даны также в списке дополнительной литературы.

Числовая информация была первым видом информации, который начали обрабатывать ЭВМ, и долгое время она оставалась единственным видом. Поэтому не удивительно, что в современном компьютере существует большое разнообразие типов и представлений чисел. Прежде всего, это целые и вещественные числа, которые по своей сути и по представлению в машине различаются очень существенно. Целые числа, в свою очередь, делятся на числа со знаком и без знака, имеющие уже не столь существенные различия. Наконец, вещественные числа имеют два способа представления – с фиксированной и с плавающей запятой, правда, первый способ сейчас представляет в основном исторический интерес.

Мы с вами будем рассматривать типы чисел в порядке увеличения их сложности.

Беззнаковые целые числа. Хотя в математических задачах не так часто встречаются величины, не имеющие отрицательных значений, беззнаковые типы данных получили в ЭВМ большое распространение. По-видимому, главная причина состоит в том, что в самой машине и программах для нее имеется много такого рода объектов: прежде всего, адреса ячеек, а также всевозможные счетчики (количество повторений циклов, число параметров в списке или символов в тексте). К этому списку стоит добавить числа, обозначающие дату и время, размеры графических изображений в пикселях. Всё перечисленное выше всегда и во всех программах принимает только целые и неотрицательные значения.

Беззнаковые целые числа представляются в машине наиболее просто. Для этого достаточно перевести требуемое число в двоичную форму и дополнить полученный результат слева нулями до стандартной разрядности. Например, восьмиразрядное число 14 будет иметь вид

0000 1110

Это же самое число в 16-разрядном представлении будет иметь слева еще 8 нулей.

Примеры кодирования некоторых характерных чисел для случая 8 двоичных разрядов (1 байт) приведены в табл.1 (для краткости записи использована не двоичная, а шестнадцатеричная система счисления).

Таблица 1. Представление беззнаковых целых чисел

10 c/c	0	1	…	127	128	129	…	255
16 c/c	00	01	…	7F	80	81	…	FF

Не менее просто определить минимальное и максимальное значение чисел для N-разрядного беззнакового целого: минимальное состоит из одних нулей, а значит, при любом N равняется нулю; максимальное, напротив, образовано одними единицами и, разумеется, для разных N различно. Для вычисления максимально допустимого значения обычно используют формулу

Max = 2^N - 1

Ниже приведена таблица максимальных значений для некоторых практически интересных N.

Таблица 2. Максимальные значения для беззнаковых целых N-разрядных чисел

N	8	16	32	64
Max	255	65 535	4 294 967 295	18 446 744 073 709 551 615

В связи с обсуждением граничных значений определенный интерес представляет проблема перехода через эти значения. Если взять самый простой, 8-разрядный случай, то это будут действия 255+1 и 0-1. Рассмотрим их подробнее.

Для того, чтобы получить правильный результат, достаточно мысленно представить себе, что при осуществлении операции слева существует еще один дополнительный (девятый) разряд. Тогда в двоичном виде сложение 255+1 выглядит следующим образом:

+	0 1111 1111
	0 0000 0001
	---------------
	1 0000 0000

Теперь, отбросив несуществующий дополнительный разряд, получаем несколько странный, но действительно имеющий место на практике результат:

255 + 1 = 0

Часто в литературе приводится еще один способ объяснения данной не очень естественной арифметики. Говорят, что при N разрядах арифметика "выполняется по модулю" 2^N, т.е. при N=8 имеем:

(255+1) mod 256 = 256 mod 256 = 0

Аналогично, хотя и чуть-чуть сложнее, можно получить результат для другого "предельного перехода" 0-1. Для этого придется дополнительно предполагать возможность займа из добавляемого девятого разряда:

-	1 0000 0000	(*)
	0 0000 0001
	---------------
	0 1111 1111

Отсюда

0 - 1 = 255

Анализировать этот случай более строгим математическим образом не совсем корректно: мы переходим к отрицательные значениям, а как кодировать их, мы пока еще не определили.

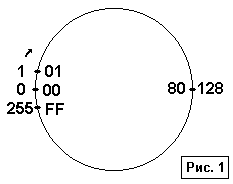Если теперь внимательно посмотреть на полученные результаты, то можно заметить, что при последовательном увеличении на единицу мы доходим до максимального значения и возвращаемся к минимальному. При вычитании единицы получается обратная картина. В книге [2], например, подобные свойства поведения чисел изображаются вместо традиционного отрезка математической числовой оси замкнутой окружностью (см. рис.1).

Обсуждаемая нами проблема выхода за отведенную разрядную сетку машины занимает важное место в реализации компьютерной арифметики и называется переполнением. Как мы видели, ситуация эта не совсем нормальная и для получения достоверных результатов ее следует избегать. Положение осложняется тем, что для процессора описанные результаты не являются чем-то "угрожающим", и он "спокойно" продолжает вычисления. Единственная тонкость заключается в том, что сам факт переполнения всегда фиксируется путем установки в единицу специального управляющего бита, который последующая программа имеет возможность проанализировать. Образно говоря, процессор "замечет" переполнение, но предоставляет программному обеспечению право принять решение реагировать на него или проигнорировать.

В ходе работы с языками программирования следует учитывать возможность переполнения. Компилятор имеет специальную опцию (в Турбо Паскале это $Q+), которая дополняет код программы специальными командами проверки переполнения. Программа естественно, становится длиннее и работает медленнее, поэтому по умолчанию контроль переполнения обычно выключен. Настоятельно рекомендуется при отладке программ включать проверку переполнения и выключать лишь после полного завершения отладки, если есть уверенность в корректной работе программы.

Примечание. При работе с Турбо Паскалем лучше использовать не $Q+, а $R+, которая дополнительно к переполнению контролирует индексы массивов и некоторые другие "потенциально опасные места".

Целые числа со знаком. Добавление отрицательных значений приводит к появлению некоторых новых свойств. Ровно половина из всех 2^N чисел теперь будут отрицательными; учитывая необходимость нулевого значения, положительных будет на единицу меньше, т.е. допустимый диапазон значений оказывается принципиально несимметричным.

Для того, чтобы различать положительные и отрицательные числа, в двоичном представлении чисел выделяется знаковый разряд. По традиции для кодирования знака используется самый старший бит, причем нулевое значение в нем соответствует знаку "+", а единичное – минусу. Подчеркнем, что с точки зрения описываемой системы кодирования число ноль (да простят меня математики!) является положительным, т.к. все его разряды, включая и знаковый, нулевые.

Представление положительных чисел при переходе от беззнаковых чисел к целым со знаком сохраняется, за исключением того, что теперь для собственно числа остается на один разряд меньше. А вот о представлении отрицательных чисел обязательно надо поговорить подробнее.

Первое, что приходит в голову, это кодировать отрицательные значения точно так же, как и положительные, только добавлять в старший бит единицу. Подобный способ кодирования называется прямым кодом. Несмотря на свою простоту и наглядность, для представления целых чисел он не получил применения в ЭВМ. Главной причиной является то, что, хотя сам код прост, действия над представленными в нем числами выполняются достаточно сложно. Поэтому для практической реализации кодирования отрицательных чисел используется другой метод, который и будет описан далее.

В его основе лежит запись отрицательных чисел в виде

2^N - |m|
где N, как обычно, количество двоичных разрядов, а m – значение числа. Поскольку фактически вместо числа теперь записывается его дополнение до некоторой характерной величины 2^N, то такой код назвали дополнительным. Фактически мы уже получали дополнительный код числа –1, когда рассматривали нижнюю границу целых чисел без знака (см. вычисления, помеченные знаком (*)). Однако способ расчета, вытекающий непосредственно из определения, не слишком хорош, поскольку требует от конструкции процессора дополнительного разряда. Поэтому для практического получения кода отрицательных чисел используется следующий эквивалентный алгоритм. Для преобразования отрицательного числа в дополнительный код необходимо:

• модуль числа перевести в двоичную форму;
• проинвертировать каждый разряд получившегося кода, т.е. заменить единицы нулями, а нули – единицами (попутно заметим, что такой код называется обратным);
• к полученному результату обычным образом прибавит единицу.

Например, переведем число –8 в двоичный 8-разрядный код. Возьмем модуль числа и дополним его до необходимого числа разрядов нулями слева:

0000 1000
Теперь проинвертируем:
1111 0111
и, наконец, прибавим единицу. Получим окончательный ответ
1111 1000

Для проверки правильности перевода можно сложить последнее число с исходным и убедиться в том, что результат будет нулевым (единицей переноса из старшего разряда, как обычно, пренебрегаем).

Представление некоторых характерных 8-разрядных значений чисел приведены (в шестнадцатеричной форме) в табл.3.

Таблица 3. Представление целых чисел со знаком

10 c/c	-128	-127	…	-1	0	1	…	127
16 c/c	80	81	…	FF	00	01	…	7F

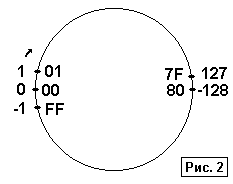
При анализе таблицы обязательно обратите внимание на скачок при переходе от –1 к 0 и граничные значения 127 и –128. "Кольцо" рис.1 для чисел со знаком преобразуется к виду, приведенному на рис.2. Предлагаем читателям самостоятельно проанализировать оба рисунка, а также дополнительно содержимое таблиц 1 и 3. Особо подчеркнем, что сравнение кодов более 7F₁₆ для чисел с учетом и без учета знака дает разные результаты. Например, для беззнаковых чисел 81₁₆ (129₁₀) определенно больше, чем 7F₁₆ (127₁₀). Для чисел со знаком, наоборот, отрицательное значение 81₁₆ (-127₁₀) будет, бесспорно, меньше, чем 7F₁₆ (127₁₀).

При проведении описываемого нами сопоставления некоторую помощь может оказать табл.4.

Таблица 4. Сравнение представления целых чисел без знака и со знаком

код	0	1	2	…	7F	80	81	…	FE	FF
без знака	0	1	2	…	127	128	129	…	254	255
со знаком	0	1	2	…	127	-128	-127	…	-2	-1

Наконец, еще один результат сравнения чисел со знаком и без него состоит в том, что общее количество их значений одинаково, но их диапазоны сдвинуты вдоль числовой оси:

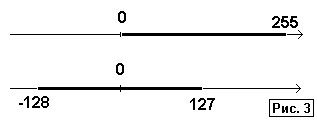
Большая часть наших рассуждений была построена на базе 8-разрядных чисел. Это ни в коей мере не ограничивает общности полученных выводов. Единственно, что достаточно сильно количественно зависит от числа разрядов N, так это граничные значения чисел Max и Min, значения которых приведены в таблице 5.

Таблица 5. Максимальные и минимальные значения для целых N-разрядных чисел со знаком

N	8	16	32	64
Max	127	32767	2 147 483 647	9 223 372 036 854 775 807
Min	-128	-32768	-2 147 483 648	-9 223 372 036 854 775 808

Хотя дополнительный код гораздо менее наглядный, чем прямой, он позволяет значительно проще реализовать арифметические операции. Более того, наличие дополнительного кода позволяет упразднить действие вычитания, сводя его к сложению с дополнительным кодом вычитаемого.

Завершить изложение данной части вопроса хочется цитатой из книги известного российского специалиста по разработке ЭВМ Н.П. Бруснецова:

"к понятию дополнительного кода, … весьма неудобному для человеческого восприятия, можно подойти естественным путем, выполняя … вычитание из меньшего числа большего. Этот подход не избавляет от неудобств, но может служить определенным утешением, так как показывает, что неудобства не придуманы людьми, а являются неотъемлемым свойством двоичного представления чисел"

(см. книгу [1] в списке дополнительной литературы).

Вещественные числа. Разобравшись с представлением целых чисел, перейдем к числам, содержащим дробную часть. Повторяя основные принципы представления информации (см. билет 10), мы уже подчеркивали принципиальное отличие между вещественными и целыми числами: целые числа дискретны, и отсюда (если не брать во внимание эффект переполнения) каждому целому числу соответствует уникальный двоичный код; вещественные числа, напротив, непрерывны, а значит, не могут быть полностью корректно перенесены в дискретную по своей природе вычислительную машину. Это означает, что некоторые вещественные числа, незначительно отличающиеся друг от друга, могут иметь одинаковый код.

Отбрасывание младших двоичных разрядов при переходе ко внутреннему двоичному представлению приводит к появлению специфической "машинной" погрешности. Например, если запустить программу

PROGRAM paradox;
VAR x,y: REAL; i: INTEGER;
BEGIN x:=1; y:=0;
    FOR i:=1 TO 10 DO y:=y+0.1;
    IF x=y THEN writeln('x равно y')
        ELSE writeln('x не равно y');
    writeln('разность x и y равна', x-y);
END.
то она, как ни удивительно с точки зрения математики, сообщит, что X не рано Y. Языки программирования никакого отношения к приведенному механизму погрешности не имеют; подобный эксперимент может быть произведен с любым из них, просто чем больше разрядов используется в представлении чисел, тем, возможно, сложнее будет эффект сделать видимым.

В любой книге по вычислительной технике сказано, что существует два способа представления вещественных чисел: с фиксированной и с плавающей запятой. Однако в связи с тем, что первый способ сейчас практически не используется, найти понятное его описание в современных учебниках довольно трудно. В частности, в процессе подготовки материала автор этих строк пользовался по данному вопросу достаточно старой монографией [2] из списка дополнительной литературы. Именно по причине слабого представления в современной литературе, рассмотрим здесь форму представления вещественных чисел с фиксированной запятой подробнее, чем она, возможно, того заслуживает.

Итак, в старых машинах, использовавших фиксированное размещение запятой, положение последней в разрядной сетке ЭВМ было заранее обусловлено – раз и навсегда для всех чисел и для всех технических устройств. Поэтому отпадала необходимость в каком-либо способе ее указания во внутреннем представлении чисел. Все вычислительные алгоритмы были заранее "настроены" на это фиксированное размещение.

Но в практических задачах встречаются самые разнообразные по величине числа. Как же их втиснуть в "прокрустово ложе" с фиксированной запятой? Для этого программист, подготавливая задачу к решению на ЭВМ, проделывал большую предварительную работу по анализу величины данных и их масштабированию: маленькие числа умножались на определенные коэффициенты, а большие, напротив, делились. Масштабы подбирались так, чтобы результаты всех операций, включая промежуточные, не выходили за пределы разрядной сетки и, в то же время, обеспечивали максимально возможную точность (об этом чуть позднее). Тщательная подготовительная работа требовала много времени и часто являлась источником ошибок. Во всяком случае, из сказанного очевидно, что каждая задача помимо собственно программирования требовала большой специализированной подготовки данных к обработке на данной конкретной ЭВМ.

А теперь несколько слов о проблеме точности, уже упоминавшейся выше. Поскольку чаще всего запятая фиксировалась перед самым старшим из разрядов, что было очень удобно для умножения, то масштабы для чисел обычно выбирались так, чтобы сделать их как можно ближе к единице. С другой стороны, то, что хорошо при умножении, угрожало выйти за пределы разрядной сетки, скажем, при сложении! Словом, едва ли кто-нибудь из читателей будет сожалеть о том, что мы сейчас избавлены от всего этого…

Примечание. Раньше, рассказывая о фиксированном и плавающем размещении запятой, автор часто ссылался на разные типы калькуляторов, использовавших те или иные формы представления результата на табло. Но современные школьники, скорее всего, уже не видели калькуляторов с фиксированным размещением запятой, так что данный наглядный способ объяснения тоже безвозвратно ушел.

Итак, подробное рассмотрение представления чисел с фиксированным размещением запятой не только показало его недостатки, но и неявно наметило путь их устранения. В самом деле, если наиболее сложным и трудоемким местом является масштабирование данных, надо его автоматизировать. Иными словами, надо научить машину самостоятельно размещать запятую так, чтобы числа при счете по возможности не выходили за разрядную сетку и сохранялись с максимальной точностью. Для этого, разумеется, придется разрешить ЭВМ "перемещать" запятую, а значит, дополнительно как-то сохранять в двоичном представлении числа ее текущее положение. В этом, собственно, и заключается представление чисел с плавающей запятой.

Интересно, что удобное представление вещественных чисел не пришлось специально придумывать. В математике уже существовал подходящий способ записи, основанный на том факте, что любое число A в системе счисления с основанием Q можно записать в виде

A = (±M) * Q ^±P ,
где M называют мантиссой, а показатель степени P - порядком числа. Для десятичной системы это выглядит очень привычно, например: заряд электрона равен -1,6*10^-19 к, а скорость света в вакууме составляет 3*10⁸ м/сек.

Некоторое неудобство вносит тот факт, что представление числа с плавающей запятой не является единственным:

3*10⁸ = 30*10⁷ = 0,3*10⁹ = 0,03*10¹⁰ = ...

Поэтому договорились для выделения единственного варианта записи числа считать, что мантисса всегда меньше единицы, а ее первый разряд содержит отличную от нуля цифру – в нашем примере обоим требованиям удовлетворит только число 0,3*10⁹. Описанное представление чисел называется нормализованным и является единственным. Любое число может быть легко нормализовано.

Особо подчеркнем, что требования к нормализации чисел вводятся исходя из соображений обеспечения максимальной точности их представления. Наиболее внимательные читатели справедливо усмотрели здесь связь с разговором о выборе оптимального масштаба для машин с фиксированной запятой, который был приведен несколько ранее.

Все сказанное о нормализации можно применять и к двоичной системе:

A = (± M) * 2 ^±P,   причем ½ ≤ M <1.

Например: -3₁₀ = -0,11*2¹⁰: M=0,11 и P=10. Существенно, что двоичная мантисса всегда начинается с единицы (M ≥ ½). Поэтому во многих ЭВМ эта единица не записывается в ОЗУ, что позволяет сохранить еще один дополнительный разряд мантиссы (так называемая скрытая единица).

Арифметика чисел с плавающей запятой оказывается заметно сложнее, чем с фиксированной. Например, чтобы сложить два числа с плавающей запятой, требуется предварительно привести их к представлению, когда оба порядка равны; такую процедуру принято называть выравниванием порядков. Кроме того, в результате вычислений нормализация часто нарушается, а значит необходимо ее восстанавливать. Тем не менее, вычислительные машины со всем этим великолепно умеют автоматически справляться, и именно такой способ вычислений лежит в основе работы современных компьютеров. Заметим, что для процессоров Intel все операции с плавающей точкой вынесены в специальный блок, который принято называть математическим сопроцессором (до 486 модели сопроцессор конструктивно представлял собой отдельную микросхему). Представление чисел в языках высокого уровня, как правило, ориентируется на таковое в сопроцессоре.

Таким образом, мы видим, что при использовании метода представления вещественных чисел с плавающей запятой фактически хранится два числа: мантисса и порядок. Разрядность первой части определяет точность вычислений, а второй – диапазон представления чисел.

К описанным выше общим принципам представления вещественных чисел необходимо добавить правила кодирования мантиссы (особенно отрицательной) и порядка. Эти правила могут отличаться для различных машин. Для IBM PC мантисса хранится в прямом коде, а для хранения порядка используется так называемый сдвиг: к значению порядка прибавляется некоторая константа (например, для типа REAL в Паскале она равна 80₁₆ [2], [5]). В результате все значения порядка будут положительными беззнаковыми числами и, как указано в [2], "при описанном представлении порядка … упрощается операция сравнения произвольного числа с нулем, которая выполняется аппаратно довольно часто". Интересно, что не все двоичные комбинаций для вещественных чисел соответствуют "правильным" числам [6]: некоторые из них кодируют бесконечные значения, а некоторые – нечисловые данные (NaN – not a number). Подобные "неправильные" данные обрабатываются по специальным правилам.

Таким образом, если сравнить между собой представление целых и вещественных чисел, то станет отчетливо видно, как сильно различаются числа, скажем, 3 и 3.0. Поэтому не стоит удивляться тому, что в языках программирования проблема перевода чисел из одной формы в другую имеет определенные особенности.

Методические комментарии для учителей. В статье систематически изложены наиболее важные принципы хранения различных типов числовой информации в ЭВМ. Как обычно, материал гораздо более подробный, чем это необходимо для ответа "среднестатистическому" ученику, поэтому учитель, руководствуясь уровнем подготовки своих выпускников, для проведения экзамена просто выберет некоторое подмножество из изложенных выше сведений. По мнению автора, прежде всего можно почти полностью исключить материал о фиксированном размещении запятой в вещественных числах, поскольку он в основном представляет исторический характер (хотя и способствует более глубокому пониманию проблемы). Следующим "кандидатом на сокращение" являются целые числа без знака, хотя об этом типе данных минимальное количество сведений желательно все же оставить. Кроме того, можно уменьшить некоторое количество подробностей о принципах хранения вещественных чисел.

При описании общих принципов представления чисел практически нигде не делалось конкретизации по типам данных какого-либо языка программирования. А между тем, в языках имеются определенные особенности хранения чисел, в том числе часто возможно несколько типов целых и вещественных данных разной длины. "Подгоняя" опубликованные здесь материалы под содержание своего курса информатики, учителя вправе заменить некоторые второстепенные общие принципы вопросами представления числовых данных в том языке, который изучался. Как это можно сделать, например, для Паскаля, демонстрирует статья [5].

Возможно, некоторые сочтут субъективной позицию авторов, не включивших в материалы данного билета алгоритмы перевода "10 => 2" и "2 ==> 10" (предполагается, что для этого есть вопрос в предыдущем билете). Строго говоря, первое предложение в вопросе данного билета может при изолированном рассмотрении быть истолковано и как необходимость объяснить основы двоичного кодирования, в том числе, и перевод в двоичную систему счисления. Тем не менее, мы считаем целесообразным именно такое разделение материала, как приведено выше.

Не стоит исключать из требований к ответам учеников подготовку таблиц, подобных приведенным в статье, руководствуясь только тем, что их, "трудно запомнить". Зато, если понимаешь материал, их можно очень быстро построить! Достаточно запустить программу-калькулятор Windows и любая таблица будет получена менее чем за несколько минут. Про электронные таблицы и говорить не приходится…

Основная литература

1. Семакин И., Залогова Л., Русаков С., Шестакова Л.. Информатика. Учебник по базовому курсу. М.: Лаборатория Базовых Знаний, 1998, 464 с.
2. Андреева Е., Фалина И. Информатика: Системы счисления и компьютерная арифметика. М.: Лаборатория Базовых Знаний, 1999, 256 с.

Дополнительная литература

1. Бруснецов Н.П. Микрокомпьютеры. М.: Наука, 1985, 208 с.
2. Карцев М.А. Арифметика цифровых машин. – М.: Наука, 1969. – 576 с.
3. Толстых Г.Д. Числа в математике, физике и информатике. / Информатика и образование, 1997, N 8, с.36-40
4. Толстых Г.Д. Представление чисел: от абака до компьютера. / Информатика и образование, 1998, N 1, с.43-47
5. Еремин Е.А. Представление информации в ЭВМ средствами Turbo Pascal / Информатика и образование, 1999, N 3, с.47-58
6. Бродин В.Б., Шагурин И.И. Микропроцессор i486. Архитектура, программирование, интерфейс. – М.: Диалог-МИФИ, 1993. – 240 с.